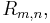Dickson's lemma

In mathematics, Dickson's lemma is a finiteness statement applying to n-tuples of natural numbers. It is a simple fact from combinatorics, which has become attributed to the American algebraist L. E. Dickson. It was certainly known earlier, for example to Gordan in his researches on invariant theory.

Stating it first for clarity for N², for any pair (m,n) of natural numbers we can introduce

$R_{m,n},\$

the 'rectangle' of numbers (r, s) with r at least m and s at least n. This is semi-infinite in the north and east directions, in the usual plane representation. The lemma then states that any union of the R_m,n can be expressed as the union of a finite subset of those R_m,n. This is analogous to the conventional topological definition of compactness.

The generalization to N^k is the natural one, with k-tuples in place of pairs.

The statement says something about N^k as the topological space with the product topology arising from N, where the latter has the (semi-continuity) topology in which the open sets are all sets R_m defined as all n with n at least m. The 'rectangles' are by definition a base for the topology; it says finite unions give all open sets.

As for the proof of the lemma, it can be derived directly, but a slick way is to show that it is a special case of Hilbert's basis theorem. In fact it is essentially the case of ideals generated by monomials.

References

Dickson, L. E. (1913). "Finiteness of the odd perfect and primitive abundant numbers with $n$ distinct prime factors". Amer. Journal Math. 35 (4): 413–422. doi:10.2307/2370405. JSTOR 2370405.